Hiroki Naganuma

Questions

Q1 Global Minima は 1 つか？

ひとつじゃない

確率的最適化は大域的収束をするのか

• 制約付き最適化

• “確率的最適化”を読む前に知っておくといいかもしれない関数解析のこと

• 擬似凸函数
• 確率的勾配降下法のメリットについて考えてみた

『最急降下法では、局所解から逃げることはできないが、確率的勾配降下法（stochastic gradient）は乱数の挙動のおかげで局所解から脱出することができる』と書かれています。確かに、「確率的勾配降下法が局所解に陥らないことを断言はできないが、それでも脱出できる可能性はある」　

Q2 必要条件として、勾配の SUM が 0 であることで十分か？

線形回帰などを仮定したら、損失関数が凸であれば、局所解 = 大域的最適解で、十分な条件

• 狭義凸関数

• 降下法

• Ioannis のコースの動画

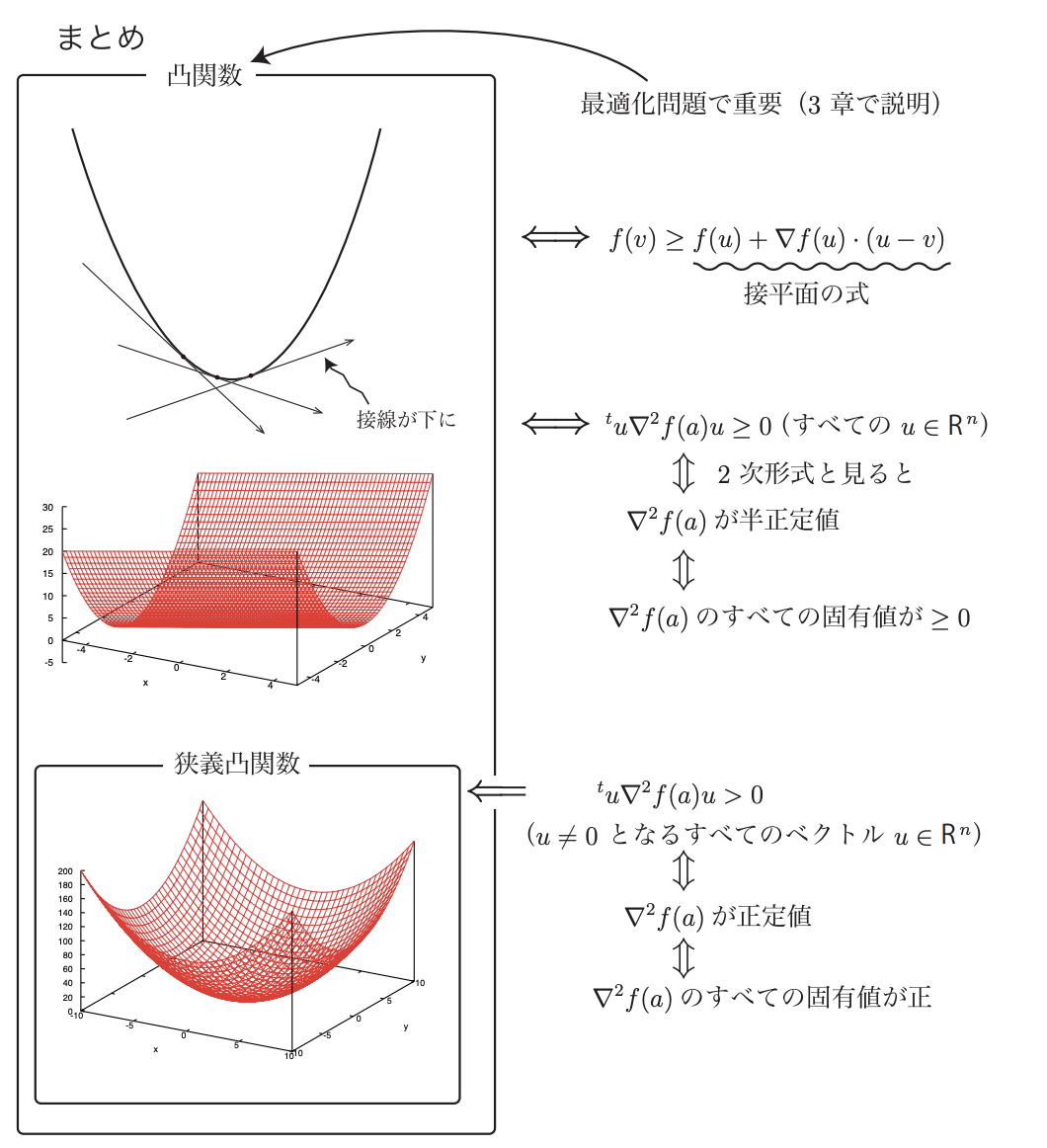
• ロジスティック回帰のコスト関数が凸関数であることについて

  ロジスティック回帰のコスト関数は凸関数である。線形回帰の最小二乗法のようにコスト関数を定義した場合は凸関数とはならないが、最小二乗法とは別にコスト関数を定義することで凸関数にすることができる。ロジスティック回帰のコスト関数は凸関数なので、局所解＝最適解となることが保証される。凸関数である前提を守る限り、ロジスティック回帰で局所解にハマったから…という議論は成り立たない（局所解があるなら前提が守られていないか、なにか別の原因がある）。

• 凸性を理解する：勾配降下が線形回帰に機能する理由

Q3　Counter Example (grad != 0)

• リプシッツ連続性など

Q4 Why MSE is reasonable?

• Private Video
• Universal Approximation Theorem(普遍性定理)

Q5 Bound of the Eigenvalues

• 狭義凸関数

• テイラーの定理

• Ioannis のコース
• 強凸関数・平滑関数

Q6 Simple formula transformation

Q7 Formula transformation (Strong Convexity and Expectation)

Q8 The sequence E[∥θt − θ∗∥^2] converges geometrically to 0.

Answer

• 21A_Q2
• Note

Refrence

Interpolation

Interpolation is a method of creating new data points within the range of known data points. https://www.ml-science.com/interpolation

多くの場合、そのデータポイントにフィットする関数を考え、関数ドメインのどの点でも補間値を思いつくようにすることが、より早く、より正確にデータを思いつく方法となります。 補間とは、あるデータセット内の情報を使って、経験則に基づいた推測をすることです。手元にある情報を使っての「最良の推測」です。

What is Interpolation?
Interpolation is making an educated guess with the information within a certain data set. It is a “best guess” using the information you have at hand. 

https://deepai.org/machine-learning-glossary-and-terms/interpolation

• Numerical Optimization: とてもよくまとまってる

• 東北大 数理計画法 第13回

• マクローリン展開の定義 Maclaurin expansion : 定義域全ての点 a において，その十分近くでテイラー展開可能な関数を解析的 (analytic) であるという。